Altın Oran Örnekleri
Altın Oran Örnekleri, Altın oran, doğada sayısız canlı veya cansız varlıkların şekillerinde veya yapısında bulunan özel bir değerdir. Doğada bir bütünün parçaları arasında gözlemlenen, yüzyıllarca sanat ve mimaride uygulanmış, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Doğada en belirgin örneklerine insan vücudunda, deniz kabuklarında ve ağaç dallarında rastlanır. Platon'a göre kozmik fiziğin anahtarı bu orandır.
Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır. Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır. Altın Oran, CB/AC= ab/CB=1.618; bu oranın değeri her ölçü için 1.618dir. Bir doğru parçanın (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki, küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB) oranına eşit olsun. Altın Oranın ifade edilmesi için kullanılan sembol, Fi 'dir. Altın Oran, pi(?) gibi iirasyonel bir sayıdır ondalık sistemde yazılışı, 1.61803398874984...'tür. (noktadan sonraki ilk 15 basamak) Altın oran için(fi) sembolü ilk kez 1909 yılında Amerikalı matematikçi Mark Barr tarafından, altın oranı kendi çalışmasında sürekli olarak kullanan Büyük Yunan heykeltıraşı Phidias'ın (M.Ö. 490?-420?) adındaki ilk Yunan harfi nedeniyle, kullanılmıştır. Bunlar dışında vücudumuzda yer alan diğer bazı altın oran örnekleri şöyledir,
İnsan bedeninde Altın Oran Örnekleri
Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır. Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır. Altın Oran, CB/AC= ab/CB=1.618; bu oranın değeri her ölçü için 1.618dir. Bir doğru parçanın (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki, küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB) oranına eşit olsun. Altın Oranın ifade edilmesi için kullanılan sembol, Fi 'dir. Altın Oran, pi(?) gibi iirasyonel bir sayıdır ondalık sistemde yazılışı, 1.61803398874984...'tür. (noktadan sonraki ilk 15 basamak) Altın oran için(fi) sembolü ilk kez 1909 yılında Amerikalı matematikçi Mark Barr tarafından, altın oranı kendi çalışmasında sürekli olarak kullanan Büyük Yunan heykeltıraşı Phidias'ın (M.Ö. 490?-420?) adındaki ilk Yunan harfi nedeniyle, kullanılmıştır. Bunlar dışında vücudumuzda yer alan diğer bazı altın oran örnekleri şöyledir,
İnsan bedeninde Altın Oran Örnekleri
- Parmak ucu-dirsek arası / El bileği-dirsek arası,
- Omuz hizasından baş ucuna olan mesafe / Omuz hizasından baş ucuna olan mesafe,
- Göbek-baş ucu arası mesafe / Omuz hizasından baş ucuna olan mesafe,
- Göbek-diz arası / Diz-ayak ucu arası.
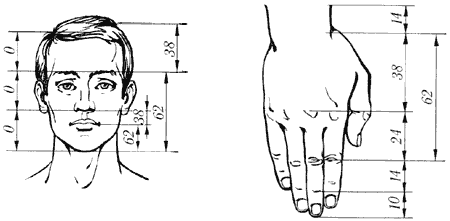
- Yüzün boyu / Yüzün genişliği,
- Dudak-kaşların birleşim yeri arası / Burun boyu,
- Yüzün boyu / Çene ucu-kaşların birleşim yeri arası,
- Ağız boyu / Burun genişliği,
- Burun genişliği / Burun delikleri arası.
- Göz bebekleri arası / Kaşlar arası.
Altın Oran Tarihi
Altın Oran, matematikte ve fiziksel evrende ezelden beri var olmasına rağmen, insanlar tarafından ne zaman keşfedildiğine ve kullanılmaya başlandığına dair kesin bir bilgi mevcut değildir. Tarih boyunca birçok defa yeniden keşfedilmiş olma olasılığı kuvvetlidir.
Leonardo da Vinci'nin günlüklerinin birinde bulunan, insan ve doğayı birbiriyle ilgilendirme-bütünleştirme çalışması için bir dönüm noktası kabul edilen ve insan vücudundaki oranları gösteren Vitruvius Adamı çalışması (1492).
Euclid (M.Ö. 365 – M.Ö. 300), "Elementler" adlı tezinde, bir doğruyu 1.6180339... noktasından bölmekten bahsetmiş ve bunu, bir doğruyu ekstrem ve önemli oranda bölmek diye adlandırmıştır. Mısırlılar keops Piramidi'nin tasarımında hem pi hem de phi oranını kullanmışlardır. Yunanlılar, Parthenon'un tüm tasarımını Altın Oran'a dayandırmışlardır. Bu oran, ünlü Yunanlı heykeltraş Phidias tarafından da kullanılmıştır. Leonardo Fibonacci adındaki İtalyan matematikçi, adıyla anılan nümerik serinin olağanüstü özelliklerini keşfetmiştir fakat bunun Altın Oran ile ilişkisini kavrayıp kavramadığı bilinmemektedir.
Leonardo da Vinci, 1509'da Luca Pacioli'nin yayımladığı İlahi Oran adlı bir çalışmasına resimler vermiştir. Bu kitapta Leonardo Leonardo da Vinci tarafından yapılmış Five Platonic Solids (Beş Platonik Cisim) adlı resimler bulunmaktadır.
Bunlar, bir küp, bir Tetrahedron, bir Dodekahedron, bir Oktahedron ve bir Ikosahedronun resimleridir. Altın Oran'ın Latince karşılığını ilk kullanan muhtemelen Leonardo da Vinci 'dir. Rönesans sanatçıları Altın Oran'ı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlardır. Örneğin Leonardo da Vinci, Son Yemek adlı tablosunda, İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar Altın Oran'ı uygulamıştır. Güneş etrafındaki gezegenlerin yörüngelerinin eliptik yapısını keşfeden Johannes Kepler (1571-1630), Altın Oran'ı şu şekilde belirtmiştir: "Geometrinin iki büyük hazinesi vardır; biri Pythagoras'ın teoremi, diğeri, bir doğrunun Altın Oran'a göre bölünmesidir." Bu oranı göstermek için, Parthenon'un mimarı ve bu oranı resmen kullandığı bilinen ilk kişi olan Phidias'a ithafen, 1900'lerde Yunan alfabesindeki Phi harfini Amerika'lı matematikçi Mark Barr kullanmıştır. Aynı zamanda Yunan alfabesindekine karşılık gelen F harfi de, Fibonacci'nin ilk harfidir.
Leonardo da Vinci, 1509'da Luca Pacioli'nin yayımladığı İlahi Oran adlı bir çalışmasına resimler vermiştir. Bu kitapta Leonardo Leonardo da Vinci tarafından yapılmış Five Platonic Solids (Beş Platonik Cisim) adlı resimler bulunmaktadır.

Bunlar, bir küp, bir Tetrahedron, bir Dodekahedron, bir Oktahedron ve bir Ikosahedronun resimleridir. Altın Oran'ın Latince karşılığını ilk kullanan muhtemelen Leonardo da Vinci 'dir. Rönesans sanatçıları Altın Oran'ı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlardır. Örneğin Leonardo da Vinci, Son Yemek adlı tablosunda, İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar Altın Oran'ı uygulamıştır. Güneş etrafındaki gezegenlerin yörüngelerinin eliptik yapısını keşfeden Johannes Kepler (1571-1630), Altın Oran'ı şu şekilde belirtmiştir: "Geometrinin iki büyük hazinesi vardır; biri Pythagoras'ın teoremi, diğeri, bir doğrunun Altın Oran'a göre bölünmesidir." Bu oranı göstermek için, Parthenon'un mimarı ve bu oranı resmen kullandığı bilinen ilk kişi olan Phidias'a ithafen, 1900'lerde Yunan alfabesindeki Phi harfini Amerika'lı matematikçi Mark Barr kullanmıştır. Aynı zamanda Yunan alfabesindekine karşılık gelen F harfi de, Fibonacci'nin ilk harfidir.
Altın Oran, bir sayının insanlık, bilim ve sanat tarihinde oynadığı inanılmaz bir roldür. Phi, evren ve yaşamı anlama konusunda bizlere yeni kapılar açmaya devam etmektedir. 1970'lerde Roger Penrose, o güne kadar imkânsız olduğu düşünülen, "yüzeylerin beşli simetri ile katlanması"nı Altın Oran sayesinde bulmuştur.
Altın Oranını Kullanıldığı Yerler
1. Ayçiçeği: Ayçiçeğinin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının bir birine oranı, altın oranı verir.
2. Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.
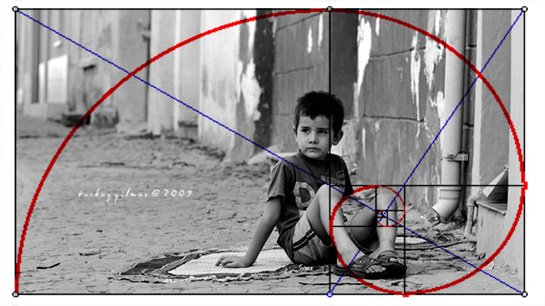
3. İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. Işte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.
4. İnsan Vücudu: İnsan Vücudunda Altın Oranın nerelerde görüldüğüne bakalım:
4.1. Kollar: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölümünün alt bölüme oranı altın oranı verceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.
4.2. Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. Işte size alaka... Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.
5. Tavşan: İnsan kafasında olduğu gibi tavşanda da aynı özellik vardır.
6. Mısır Piramitleri: Her bir piramitin tabanının yüksekliğine oranı yine altın oranı veriyor.
7. Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş olduğu tabloları inceleyelim.
7.1. Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir.
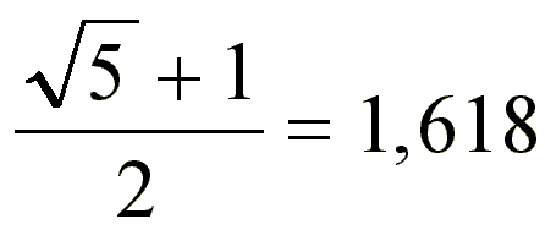
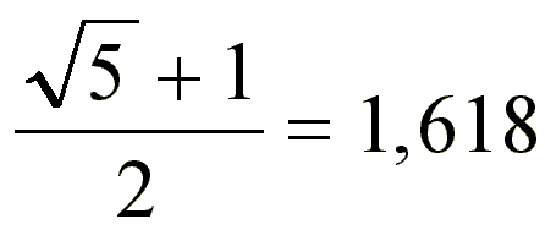
7.2. Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.
8. Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.
9. Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu eğrinin eğrilik açısı altın orandır.
10. Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de koleksiyon yapanımız vardır. İşte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.
11. Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.
12. Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otunda da vardır.
13. Elektrik Devresi: Altın Oran sadece Matematik ve kainatta değil,
Fizik te de kullanılıyor. Verilen ne tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş= yani altın oran olur.
14. Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (-ki biz bu dikdörtgene altın dikdörtgen diyoruz.-) İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.
15. MİMAR SINAN: Mimar Sinanın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camilerinin minarelerinde bu oran görülmektedir.
İnsan Vücudunda Altın Oran
İnsan vücudunda altın oran, köklü bir geçmişe sahip, uzun yıllardır bilim adamlarından, tasarımcılara kadar birçok kişi tarafından farklı sektörlerde yararlanılan bir ölçü parametresidir. Kökleri 1170 ve 1240 yılları arasında yaşamış olan orta çağın en yetenekli matematikçisi olarak bilinen Fibonacci'e dayanır. Fibonacci'nin bulmuş olduğu, altın oran ya da Fibonacci dizini adıyla anılan bu ölçü sistemi temel olarak her sayının kendinden bir önceki ile toplanması nihayetinde oluşturulan bir dizindir. Örneğin; 0, 1, 1, 2, 3, 5, 8, 13, 21, ... gibi. Bu şekilde devam eden bir dizin bir süre sonra sürekli aynı farkı verir. Bu fark da 1,618'dir ve altın oran olarak bilinir.
Altın oran daha sonraları başta Leonardo da Vinci olmak üzere bir çok sanatçı, tasarımcı ve bilim adamı tarafından farklı alanlarda farklı amaçlar için kullanılmıştır. Her alanda olduğu gibi insan vücudunda da altın orana rastlamak mümkündür. İnsan bedeni göz önünde bulundurulduğunda birçok altın oran belirtisi ortaya çıkar. Bunlardan bazıları; ayaktan dize kadar olan kısım bir birim olarak kabul edildiğinde ardı ardına toplamı insan vücudunda tam olarak göbeğe denk gelir. Bu bir altın orandır ve bize 1,618 sonucunu verir. Başın üst kısmından boyna kadar olan kısmın ardı ardına toplamı da göbeğe denk gelir ki yine bu da bir altın orandır
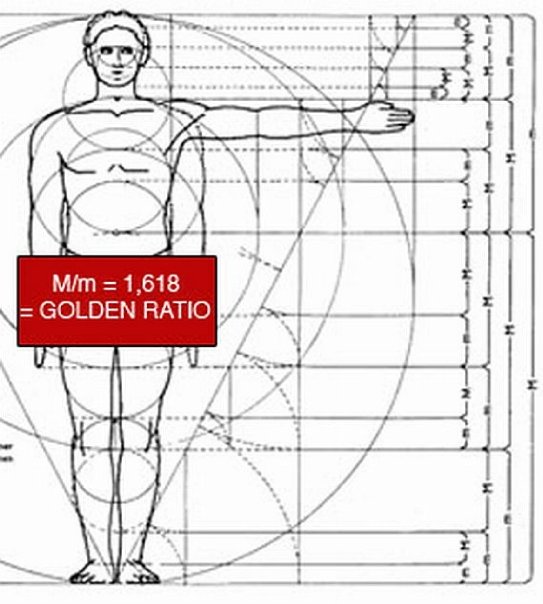
Bunlar dışında da insan vücudunda farklı noktalarda altın oran bulunmaktadır. Elde, baş parmak hariç parmakların üç boğumdan oluşması ve bu boğumların ilk ikisinin toplamının üçüncü boğumun ölçüsünü vermesi gibi. Ayrıca insan yüzünde de bazı noktalarda altın oran mevcuttur. En kolay görülebilecek olanı tavşan dişlerinin boy ve eninin birbirine eşit olması gibi. Bu da doğru ve estetik bir görüntü yaratmak isteyen diş doktorlarının işini kolaylaştıran başka bir altın orandır. Dış görünüş harici bir de iç organlarda altın orana rastlamak mümkündür. Örneğin; akciğerlerde düzensiz olarak dizilmiş şekilde görünen her kısa bronşun toplamı uzun bronşun toplamına eşittir ve aradaki fark 1 ila 1,618 civarındadır. Aynı şekilde iç kulakta yer alan ses titreşimlerinin iletilmesini sağlayan ve sarmal şeklindeki cochlea da bize altın oranı vermektedir. Tüm canlıların temel özelliklerinin depolanmasını ve aktarımını sağlayan DNA da altın orana sahiptir.

Bunlar dışında da insan vücudunda farklı noktalarda altın oran bulunmaktadır. Elde, baş parmak hariç parmakların üç boğumdan oluşması ve bu boğumların ilk ikisinin toplamının üçüncü boğumun ölçüsünü vermesi gibi. Ayrıca insan yüzünde de bazı noktalarda altın oran mevcuttur. En kolay görülebilecek olanı tavşan dişlerinin boy ve eninin birbirine eşit olması gibi. Bu da doğru ve estetik bir görüntü yaratmak isteyen diş doktorlarının işini kolaylaştıran başka bir altın orandır. Dış görünüş harici bir de iç organlarda altın orana rastlamak mümkündür. Örneğin; akciğerlerde düzensiz olarak dizilmiş şekilde görünen her kısa bronşun toplamı uzun bronşun toplamına eşittir ve aradaki fark 1 ila 1,618 civarındadır. Aynı şekilde iç kulakta yer alan ses titreşimlerinin iletilmesini sağlayan ve sarmal şeklindeki cochlea da bize altın oranı vermektedir. Tüm canlıların temel özelliklerinin depolanmasını ve aktarımını sağlayan DNA da altın orana sahiptir.
İnsan vücudu dışında kar kristallerinden, hayvanlardaki boynuzlara ve dişlere, uzay boşluğundan, salyangozlara ve kabuklu deniz hayvanlarına, mikro organizmalara kadar evrendeki birçok canlıda ve noktada altın orana rastlamak olağandır. Öyle ki Kepler altın oranın önemini vurgulamak adına "hazine" ifadesini kullanmıştır.
İnsan Yüzünde Altın Oran
İnsan yüzünde altın oran; İnsanların her biri kendisine güven duymak ve gözde olmak ister. Dış görünüşü ile fazlaca ilgilenen, mesleki anlamda ifadenin önemli olduğunu düşünen ve bu konuları araştıran herkes altın oran kelimesi ile karşılaşmıştır. İnsan yüzünde pek çok altın oran mevcuttur. Yalnız alınan bir cetvel ile bunu sabitleyebilmek ve tam ölçüte ulaşabilmek mümkün değildir. Alınmış tüm değerler bilim adamlarınca sabitleşmiş ancak ideal olarak belirlenmiş ölçüleri içermektedir.
İnsan yüzünde altın oran hesaplaması yapabilmek için bir takım kuralları bilmek gerekir. Her ideal yüz tipi tam anlamı ile bu oranlamaya karşı gelmiyor olabilir. Yapılan araştırmalar ve alınan verilere göre bu değerler ancak tam ideal kişileri hedef gösterecek olup, tüm insanlığın bu ölçülere sahip olmasını beklemek yanlış olacaktır.
İnsan Yüzünde Altın Oran Kuralları Neleri İçerir?
Söz gelimi bir kişinin üst bölgede bulunan öndeki iki adet dişin, enlerinden elde edilecek toplam ile boylarına oranlanması altın oranı ifade etmektedir.
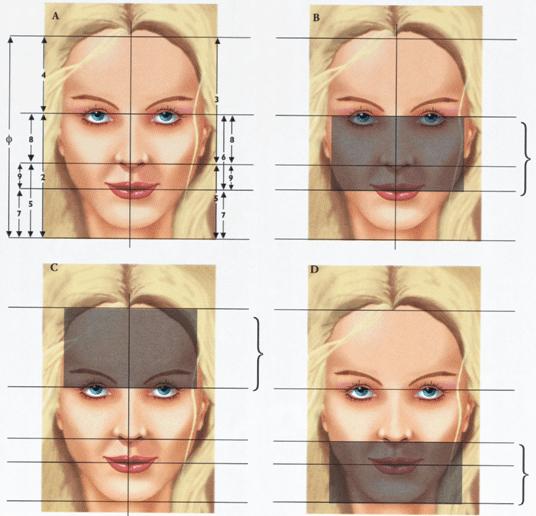
Görüldüğü gibi çokta kolay olmayan minimal hesapları işaret etmektedir. Diş doktorları için bu oranlama istenen en sağlıklı oranlamadır.
İnsan Yüzünde Altın Oran İçin Hangi Kriterler Dikkate Alınır?
İnsan Yüzünde Altın Oran Kuralları Neleri İçerir?
Söz gelimi bir kişinin üst bölgede bulunan öndeki iki adet dişin, enlerinden elde edilecek toplam ile boylarına oranlanması altın oranı ifade etmektedir.

Görüldüğü gibi çokta kolay olmayan minimal hesapları işaret etmektedir. Diş doktorları için bu oranlama istenen en sağlıklı oranlamadır.
İnsan Yüzünde Altın Oran İçin Hangi Kriterler Dikkate Alınır?
- Yüzün boyu ile yüzün genişliğinin oranlanması
- Yüzün boyu ile çene ucunun oranı ile kaşların birleştiği bölümün arası orantısı
- Göz bebeklerinin mevcut aralığı ile kaşların mevcut aralığının oranlanması
- Burun genişliği ile burun deliklerinin aralık olarak oranlanması
- Ağız boyu ile burun genişliğinin oranlanması
- Burun boyu ile dudak, ayrıca kaşların birleşim noktası aralığının oranlanması
Altın Oran Nedir
Altın oran, doğada sayısız canlı ve cansız olan varlıkların yapısında ve şeklinde bulunan özel bir oran olarak tarif edilmektedir. Ayrıca başka bir tarifte, Mısırlılar ve Yunanlılar tarafından mimaride kullanmış olan bu oran, doğada bulunan bir bütünün parçaları arasında ki gözlemlenen asırlarca mimari ve sanat alanındaki eserlerde uygulanmış, bunları uyum açısından en uygun boyutları verdiği varsayılan, sayısal ve geometrik olarak hesaplanan bir oran bağlantısı olarak kabul edilir. Bu altın oranın, doğada en belirgin bir şekilde hadsiz benzerlerine rastladığımız ve birçok varlıkta görülmektedir. Bunların başında ilk olarak gördüğünüz insan vücudu, deniz kaplumbağaları, bitkiler ve ağaç yapraklarında bu orana rastlanmaktadır. Kozmik fiziğin anahtarı hükmünde olarak, bu oran Platon tarafından gösterilmiştir. Farklı bir açıdan da altın oranı, bir dikdörtgenin eninin boyuna olan oranını, en estetik ve güzel bir şekilde açıklayan tanımlarda bulunmaktadır.
Yukarıdaki tanımlardan anladığımız kadarıyla altın oranı, kendisini böldüğü kısmın eşdeğer olarak görülmektedir. Yani her şeyin bir çifti, artısı ve eksisi olduğu gibi bu özel oranda bu gibi şeylere işaret edilmektedir.
Bu altın oranı, ilk olarak eski mısırlılar ve yunanlılar tarafından keşfedilmiş ve bu oranı mükemmel bir şekilde kendi mimarilerinde ve sanat eserlerinde kullanmışlardır.
Altın oranı sayısal açıdan ifade etmek gerekirse AO; CB/AC:AB/CB: 1.618 olarak ifade edilmektedir. Bu şekilde formüle edilen altın oranın da ifade edilmek istenen mana, bu oranlar arasındaki değer her ölçü için altın oranı olan 1.6
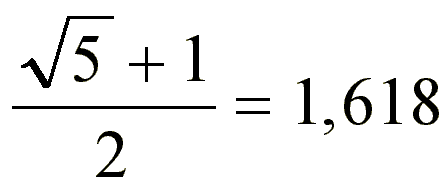
618 rakamını vermelidir.
Bu oran pi (π) sayısı gibi irrasyonel olan bir sayıdır. Ondalık olarak yazılan şekli ise: 1.6180339887498...dir. Böyle devam edilirse bu sayının 15’inci basamağından sonra bulunan ilk 15 basamak, altın oranın kısaca aynı gösterimi olacaktır. Bilim dilinde altın oranın sembol olarak gösterimi ise PHI yani Φ şeklinde gösterilmektedir.
Bu esrarengiz bir o kadar da ilginç olan bu oranı dünyanın, insanların, bitkilerin, ağaçların, kuşların ve daha birçok canlı ve cansız mahlukun üzerinde, Allah tarafından bu varlıkları yaratırken kullandığı orandır.
Ayrıca günümüzde insanlarda kullandıkları teknolojide ve yaşadığımız hayatta birçok yerde bu oran kullanmaktadır. Toplum bu oranı kısaca göz nizamının ve düzeninin oranı diye tarif edilmektedir. Göze görünen en güzel şekilde ayarlanmasıdır.
Altın oranın kullanıldığı ve görüldüğü yerler hakkında bir misal verelim.
Mesela ayçiçeğinin merkez dışarıya doğru tanelerinin sayılarını sağdan sola, soldan sağa doğru sayıldığı zaman bu arasındaki oran altın oranını vermektedir.
İnsan vücudunda ise bu oranın nasıl göründüğünü incelersek bu oranın mevcut olduğunu görürüz. Mesela kollar insan vücudunun bir parçası olarak dirsek kısmından iki bölüme ayrılmış durumdadır. Yani büyük üst kısmı ve küçük ise alt kısmı oluşturmaktadır. Kolumuzun alt bölümün üst bölüme oranı altın oranı vereceği gibi, ayrıca kolun tamamının üst kısmın oranı yine bu oranı verecektir.
Bu altın oranı, ilk olarak eski mısırlılar ve yunanlılar tarafından keşfedilmiş ve bu oranı mükemmel bir şekilde kendi mimarilerinde ve sanat eserlerinde kullanmışlardır.
Altın oranı sayısal açıdan ifade etmek gerekirse AO; CB/AC:AB/CB: 1.618 olarak ifade edilmektedir. Bu şekilde formüle edilen altın oranın da ifade edilmek istenen mana, bu oranlar arasındaki değer her ölçü için altın oranı olan 1.6
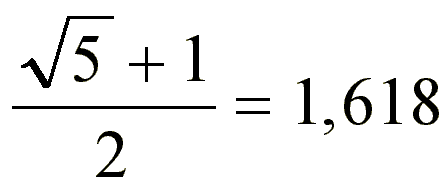
618 rakamını vermelidir.
Bu oran pi (π) sayısı gibi irrasyonel olan bir sayıdır. Ondalık olarak yazılan şekli ise: 1.6180339887498...dir. Böyle devam edilirse bu sayının 15’inci basamağından sonra bulunan ilk 15 basamak, altın oranın kısaca aynı gösterimi olacaktır. Bilim dilinde altın oranın sembol olarak gösterimi ise PHI yani Φ şeklinde gösterilmektedir.
Bu esrarengiz bir o kadar da ilginç olan bu oranı dünyanın, insanların, bitkilerin, ağaçların, kuşların ve daha birçok canlı ve cansız mahlukun üzerinde, Allah tarafından bu varlıkları yaratırken kullandığı orandır.
Ayrıca günümüzde insanlarda kullandıkları teknolojide ve yaşadığımız hayatta birçok yerde bu oran kullanmaktadır. Toplum bu oranı kısaca göz nizamının ve düzeninin oranı diye tarif edilmektedir. Göze görünen en güzel şekilde ayarlanmasıdır.
Altın oranın kullanıldığı ve görüldüğü yerler hakkında bir misal verelim.
Mesela ayçiçeğinin merkez dışarıya doğru tanelerinin sayılarını sağdan sola, soldan sağa doğru sayıldığı zaman bu arasındaki oran altın oranını vermektedir.
İnsan vücudunda ise bu oranın nasıl göründüğünü incelersek bu oranın mevcut olduğunu görürüz. Mesela kollar insan vücudunun bir parçası olarak dirsek kısmından iki bölüme ayrılmış durumdadır. Yani büyük üst kısmı ve küçük ise alt kısmı oluşturmaktadır. Kolumuzun alt bölümün üst bölüme oranı altın oranı vereceği gibi, ayrıca kolun tamamının üst kısmın oranı yine bu oranı verecektir.
Altın Oran
Altın oran, özellikle çeşitli bilim dallarında, mimari ve sanatsal alanlarda yararlanılan, belirli bir tutarlılık üzerine kurulu parçalar arasındaki uyumu yansıtan geometrik ve sayısal değerlere verilen isimdir. İlk kez Mısırlılar ve Yunanlar tarafından mimari yapılarda, heykellerde ve diğer sanatsal alanlarda kullanılmıştır. Temel olarak bölünen bir bütünün yan yana getirilen iki parçasının diğer büyük parçayı oluşturması prensibine dayanır ve altın oranın sayısal değeri 1,618'dir.
Doğada bir çok canlıda ve yapıda gözlemlenebilen altın oranın insanlar tarafından ne zaman ve nasıl bulunduğu tam olarak bilinmemekle birlikte bu konudaki en ünlü eser Leonardo da Vinci'nin 1492 yılında tamamladığı insan vücudundaki altın oranları gösteren Vitrivius Adamı isimli çalışmasıdır. Leonardo da Vinci'nin günlükleri arasında, aldığı notların yanında bulunan bu çizim iç içe geçmiş kolları ve bacakları açık ve kapalı olmak üzere çıplak bir adamı tasvir ediyordu. Çizimdeki vücut çeşitli sayısal değerlerle, geometrik şekillerle eşleştirildiğinden dolayı Leonardo da Vinci'nin "İnsanın Oranları" adını verdiği bu çizim insanı ve doğayı, aralarındaki uyumu keşfetmeye çalışan bir eser olarak tanımlanmaktadır. Altın oran ve ya ilahi oran adını kullanan ilk kişi de Leonardo da Vinci'dir. İtalyan matematikçi Fibonacci de altın orana uygun olarak dizilen sayılar topluluğunu keşfetmiştir ancak bunu altın oranın farkını bilerek yapıp, yapmadığı tam olarak bilinmemektedir. Fibonacci diziliminde arka arkaya gelen her sayının toplamı bir sonraki sayıya eşittir. Örneğin; ..., 3, 5, 8, 13. 21... gibi.
Mısırlıların Piramitleri yaparken de altın oran benzeri bir sistemden yararlandıkları gözlemlenmektedir. Keops Piramidi'nin kare şeklindeki tabanının ölçüsü ile üçgen şeklindeki yüzeyine uygun bir yuvarlak çizildiğinde bu yuvarlığın büyüklüğü birbirleri ile eşit olmaktadır. Aynı şekilde Yunanlar da heykel yapımlarının çoğunda bu orandan yararlanmışlardır. Rönesans Döneminde ise bir çok sanatçı tablolarında altın oranı kullanmıştır. Bu şekilde özellikle insan heykel ve çizimlerinde gerçeğe çok daha yakın sonuçlar elde edilmiştir.
İstiridye, salyangoz gibi canlıların kabuklarında, insan vücudundaki uzuvlar ve organlarda, DNA'da, uzayda ve daha bir çok farklı alanda altın orana rastlamak mümkündür.
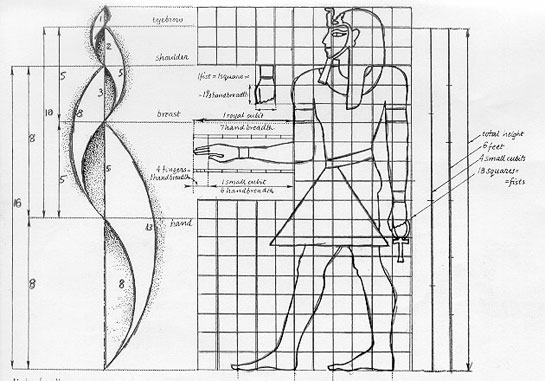
Örneğin; insan elindeki ilk 2 parmak boğumunun toplam uzunluğu 3. boğumun uzunluğuna eşittir ve ya iki ayağın toplam ölçüsü insanda yerden diz bölgesine kadar olan kısmın ölçüsüyle aynıdır. Başın üst kısmından boynun bitimine kadar olan ölçü iki kez alt alta dizildiğinde ortaya çıkan ölçü tam olarak kişinin vücudundaki merkez olan karın kısmına denk gelmektedir. Yüzde dudak bitimleri ile, göz bebekleri aynı çizgide olduğu takdirde altın oranı oluştururken bu çizginin tam ortası burnun ucuna denk gelmektedir. Akciğerde ise asimetrik şekilde gelişen kısa bronşların toplamı uzun bronşa eşittir. Salyangoz kabuğundaki ve uzay boşluğundaki spiral şekli de içten dışa doğru olmak şartıyla bu oranın kıstaslarına uymaktadır.

Örneğin; insan elindeki ilk 2 parmak boğumunun toplam uzunluğu 3. boğumun uzunluğuna eşittir ve ya iki ayağın toplam ölçüsü insanda yerden diz bölgesine kadar olan kısmın ölçüsüyle aynıdır. Başın üst kısmından boynun bitimine kadar olan ölçü iki kez alt alta dizildiğinde ortaya çıkan ölçü tam olarak kişinin vücudundaki merkez olan karın kısmına denk gelmektedir. Yüzde dudak bitimleri ile, göz bebekleri aynı çizgide olduğu takdirde altın oranı oluştururken bu çizginin tam ortası burnun ucuna denk gelmektedir. Akciğerde ise asimetrik şekilde gelişen kısa bronşların toplamı uzun bronşa eşittir. Salyangoz kabuğundaki ve uzay boşluğundaki spiral şekli de içten dışa doğru olmak şartıyla bu oranın kıstaslarına uymaktadır.
Bu oranın doğadaki canlılarda ve yapılarda var olduğu keşfedilmeden önce sırası ile ilk olarak Mısır'da özellikle Keops Piramidi'nin yapılışında kullanılmıştır. Daha sonrasında Antik Yunan Döneminde heykellerin gerçeğe daha uygun olması amacıyla bu orandan yararlanılmıştır. Rönesans döneminde de tablolarda tasvir edilen insanların ve diğer içeriklerin gerçekle örtüşmesi amacıyla altın orandan faydalanılmıştır. Ardından altın oranın geometride de var olduğu keşfedilmiştir. Başta beşgen, yıldız ve üçgen şekli olmak üzere bir çok şekilde bu oran mevcuttur hatta 1,618 ölçüsüne dayanan dikdörtgen ve üçgen şekilleri altın üçgen ve altın dikdörtgen olarak anılmaktadır. Altın üçgende tıpkı Fibonacci diziliminde olduğu gibi iki üçgenin toplam ölçüsünün bir sonraki üçgeni oluşturması şartı ile iç içe geçen üçgenlerin üst kısımlarından dışarıya doğru çizilen spiral şekli bize altın oranı vermektedir. Altın dikdörtgeni çizim şekli ise şu şekildedir: bir kare şekli çizilir, kenarlardan tekinin orta noktası karşıdaki köşelerden biriyle birleştirilir, meydana çıkan doğru yarıçap varsayılarak çizilecek çember ile dikdörtgenin yüksekliği oluşmuş olur. Diğer kenarlar da aynı şekilde tamamlandığı takdirde altın dikdörtgen elde edilmiş olur. Keops Piramidi ile benzerlikler gösteren Kepler Üçgeni ve Pentagram olarak bilinen çizgileri içten birleştirilmiş şekilde çizilen, güzelliği, estetiği ve şansı simgeleyen yıldız şekli de bir çok farklı alanda yararlanılan bir simgelerdir ve her iki şekil de altın oranla uyumlu geometrik şekillerdendir.